Hacking the Fallout Terminal Minigame
Introduction
I've always been a big fan of the Fallout series. Recently I started playing Fallout 3, and on this playthrough the terminal hacking minigame caught my interest. I realized that this minigame is actually very similar to Wordle. I recently wrote a blog post about solving Wordle, so I thought I would take a stab at solving the Fallout Terminal minigame using some of the same code.Context
For those who are unfamiliar with Fallout, terminals are computers that players can interact with in game to find information, unlock doors, or control machines, among other uses. Some terminals are locked and must be "hacked" by the player in order to get access. This is where the terminal hacking minigame comes into play.

The Rules
The player is given four attempts to guess the password out of a limited number of choices that are available on the terminal screen scattered among symbols and other characters. Each guess is given a "likeness" score, which indicates the number of characters that are correct and in the correct position. Players can then use the likeness score to rule out different passwords and continue to guess until they are correct, or they run out of guesses.Terminals have varying degrees of difficulty from "very-easy" to "very-hard". The difficulty determines the length of the words. The number of possible words depends on the stats of the player and usually falls in the range of 20 to as few as 5, however all words within the same terminal will be of the same length.
An added wrinkle is that the player can select any valid pair of brackets like(), [], {}, or <> for a bonus dud word removal or a reset of the number of attempts. For the sake of our analysis we're going to ignore the brackets.
Comparison to Wordle
For those that are familiar with Wordle, the similarities are probably already very clear. There are two key differences I want to point out. First, Fallout terminals have a fixed, limited number of known possible choices, while Wordle games have a much larger pool of over 10,000 valid guesses. This means we can treat the number of words as a constant, and not have to worry about expensive computation that scales poorly with a large number of words.
Second, Wordle gives the player three types of feedback on guesses, while Fallout only provides one. When players make a guess in Wordle, the characters can change to be green, yellow, or grey.
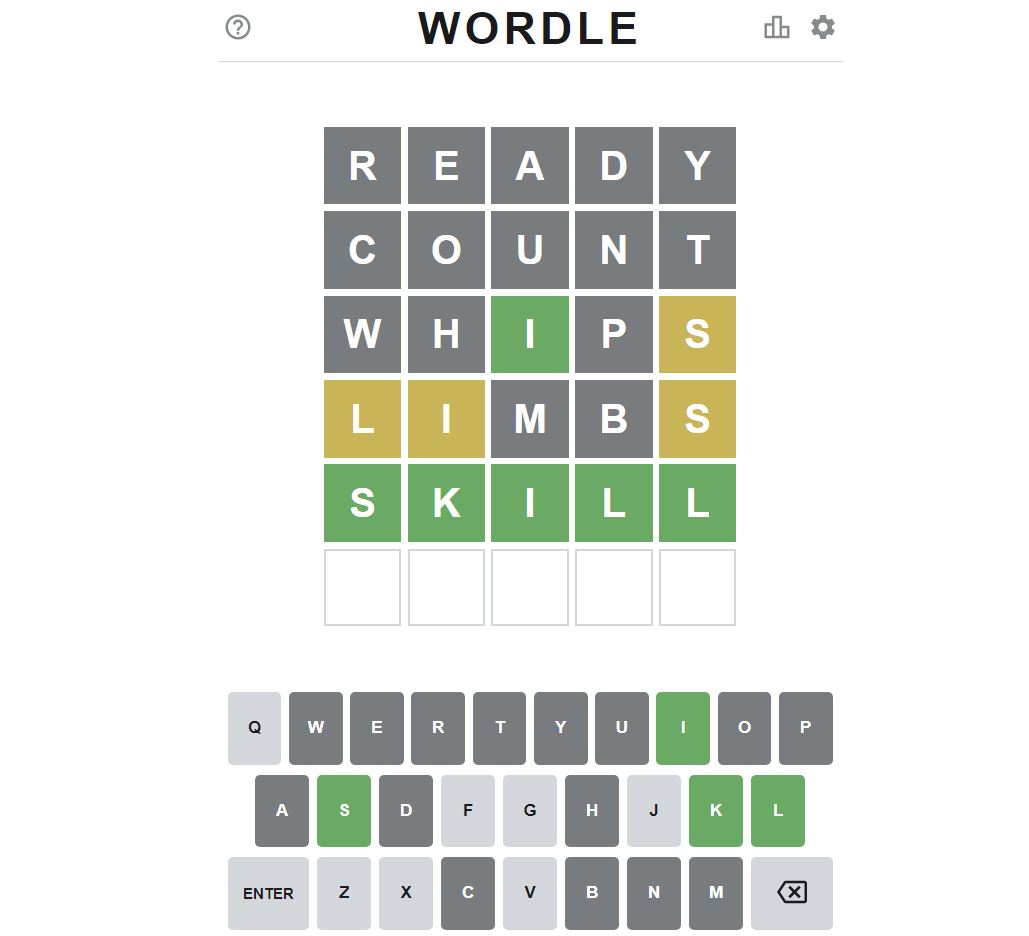
Green indicates a correct character in the correct position, yellow means a correct character in the incorrect position, and grey signals that the character is incorrect. The likeness score in Fallout only considers correct characters in the correct position. We can think of likeness in Fallout as the number of green characters in a guess in Wordle.
The most interesting difference to me is the user interface. The hacker UI of the fallout terminal along with the random symbols and hex addresses makes you feel like you are actually "hacking" the computer and cracking the passcode. The sleek, intuitive UI of Wordle, on the other hand, makes you feel like you're playing a fun little word game like a crossword puzzle with your morning coffee. It's amazing to me how these two games are nearly identical in their logical structure but feel so different.
Solving the Fallout Terminal
All the code for the terminal solver is available on Github here. You can also follow along on Google Colab here. I'm using almost the exact same code as I did for Wordle except for a few key changes:- Source of words: https://github.com/dwyl/english-words/tree/master
- Updated pruning process to eliminate words based on likeness score of previous guesses
- Improved performance visualization
- Created a new optimization strategy
Computing Likeness
To start, we can easily compute the likeness score of any two words by iterating through the characters and incrementing a counter whenever the characters at the same index match.
def get_likeness(word_a, word_b):
likeness = 0
for i in range(len(word_a)):
if word_a[i] == word_b[i]:
likeness += 1
return likenessget_likeness("rowing", "flying"), we'll get a result of 3.
Maximizing Eliminations
To explain the optimization strategy, I'll start with a basic example of five random five-letter words. In this case we have:
- swamp
- drape
- water
- swish
- again
In this strategy, the goal of our guess is to eliminate the greatest number of possible choices. Words are eliminated when they could not possibly have the same likeness score as a previous guess. To maximize eliminations, we can compute the possible likeness score of every word relative to every other word. We can keep track of this in a dictionary for each word mapping the index to the number of other words with the same character at the same index. We can then take the sum of these counts at each index, and finally choose the word with the greatest sum.
Let's trace through this algorithm, starting with "swamp" in the example above:
At index 0 we have "s", which has one match in "swish". At index 1 there is one matching "w", again in "swish". At index 2, with the character "a" we have two matches, "drape" and "again". Finally at index 3 and 4, there are zero matches for "m" and "p". That leaves us with the following dictionary mapping index to match count:
{
0: 1,
1: 1,
2: 2,
3: 0,
4: 0
}Now we'll compute the same dictionary for the other words and calculate the sums:
{'swamp': {0: 1, 1: 1, 2: 2, 3: 0, 4: 0},
'drape': {0: 0, 1: 0, 2: 2, 3: 0, 4: 0},
'water': {0: 0, 1: 0, 2: 0, 3: 0, 4: 0},
'swish': {0: 1, 1: 1, 2: 0, 3: 0, 4: 0},
'again': {0: 0, 1: 0, 2: 2, 3: 0, 4: 0}
}
{'swamp': 4, 'drape': 2, 'water': 0, 'swish': 2, 'again': 2}The maximum sum is 4, so "swamp" is the winner for the best first guess for this group of words.
Putting it all together we have the following algorithm:
def maximize_eliminations(words):
word_scores = {word: {i: 0 for i in range(len(words[0]))} for word in words}
word_sums = word_sums = {word: 0 for word in words}
for perm in permutations(words, 2):
outer_word, inner_word = perm
for i in range(len(words[0])):
if outer_word[i] == inner_word[i]:
word_scores[outer_word][i] += 1
word_sums[outer_word] += 1
return max(word_sums, key=lambda x: word_sums[x])We will use this algorithm for each guess to choose the elimination maximizing choice out of the remaining eligible options. After each guess we will prune the search space and repeat until we guess correctly.
This algorithm does not scale very well for large numbers of words. The runtime complexity isO(k*n!) where n is the number of words and k is the length of the words. The runtime grows at a factorial rate with the number of words because we have to compute the permutations of all the pairs of words.
The reason we can get away with using this algorithm for Fallout terminals is because the numeber of words is fixed and limited. This means we can treat n as a constant, and our runtime becomes O(k), which is very manageable. The word lengths also max out at 15, so the algorithm is very fast for the use case of the Fallout terminal minigame. In the example above, the runtime was 53.4 µs.
In games like Wordle, the pool of possible guesses is far larger at over 10,000 words, so this algorithm would become really slow. I ran a sample trial with 10,000 words, and the runtime was about 60 seconds.
Assessing Performance
The metrics we care about to assess the performance of this algorithm are the average number of guesses, and the percentage of terminals that are solved in four guesses or fewer. We can get a good measure of these metrics by running simulations of many terminals and looking at the results. In addition to the optimized strategy, we have a random strategy. The purpose of the random strategy is to assess how much of the performance is due to just the pruning process instead of the optimization algorithm.
Let's start with a single simulation of 10,000 trials with 20 five-letter words for both the random and optimized strategies.
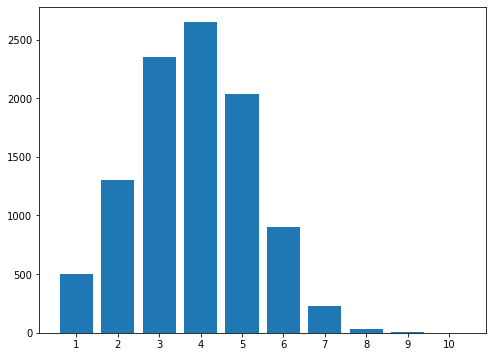
For the random algorithm we get an average of 3.78 guesses with 69% of trials solved in four guesses or fewer.
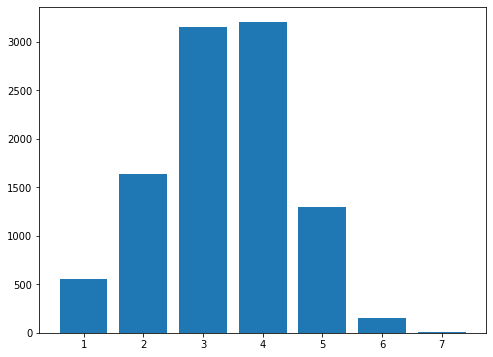
For the optimzied algorithm we get an average of 3.37 guesses with 85% of trials solved in four guesses or fewer.
That's pretty good!
Let's run some more trials and see what the trend looks like a we change the number of words and the word lengths.
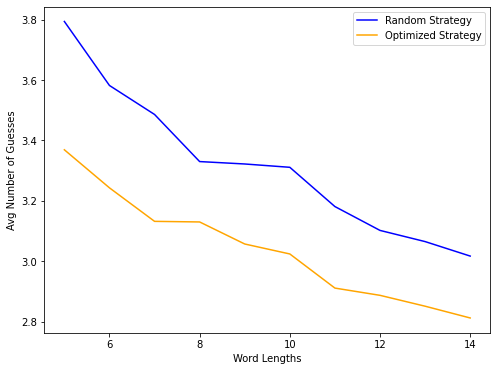
Average Number of Guesses and Word Lenghts, Holding Word Count Constant
Average Number of Guesses and Word Counts, Holding Word Lengths Constant
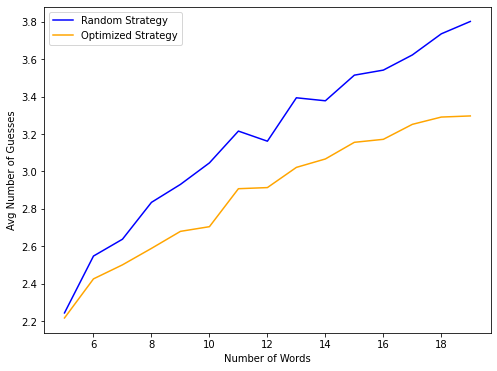
As we can see, the performance varies depending on the number of words and the length of the words. The general trend is that as we increase the lenght of words, the average number of guesses decreases, and as we increase the number of words, the average number of guesses increases.
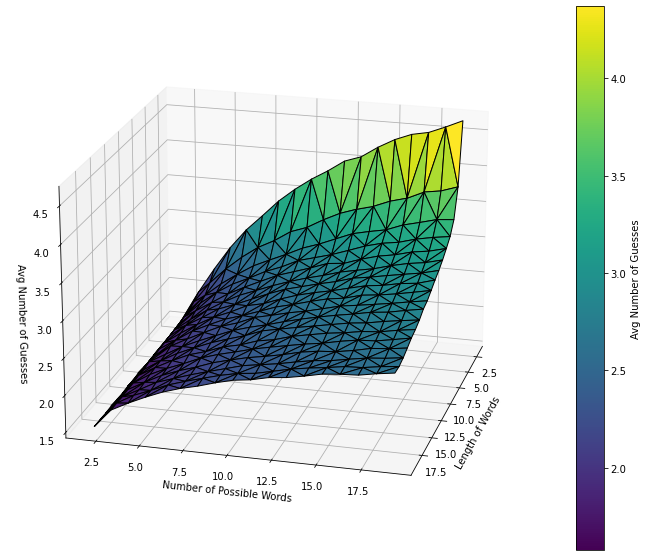
We can actually visualize this on a 3d graph where the x axis is the number of words, the y axis is the word lengths, and the z axis is the average number of guesses. You can play around with theax.view_init value for the 3d graph here to view the graphs from different angles.
Average Number of Guesses for Varying Word Lenghts and Counts
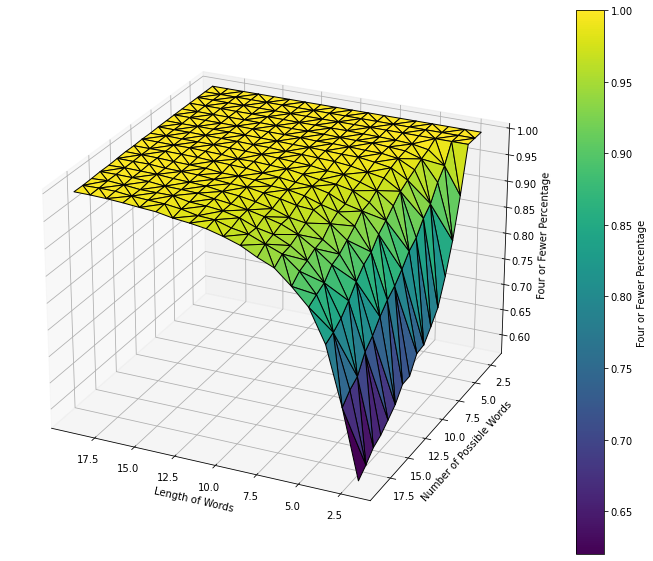
Four or Fewer Percentage for Varying Word Lenghts and Counts

Why the Difficulty Rankings are Wrong
If we think of the performance of the optimized algorithm as a proxy for the difficulty of solving the terminal, the difficulty rankings of the terminals in Fallout should actually be reversed! The "very-hard" terminals, with the longest word lengths, are actually the easiest to solve, and the "very-easy" terminals are actually the most difficult.
A true "very-hard" terminal, would be one in which there are many possible choices with a small length of 2 or 3. The hardest possible terminal, with the lowest percentage of terminals solved in four guesses or fewer, would be one where the correct password is a single character.