A Greedy Approach to Solving Wordle

Introduction

Wordle is fun, simple, and addicting, a perfect recipe for a viral web app. After growing to over 300k users, Wordle was acquired by the New York Times for around $1 million.

While I do enjoy playing Wordle, I've always been more interested in solving it with algorithms. I attempted to do this last year around this time, and I'm writing this blog post as I dive back into that code and expand on my original solution.

Framing the Problem

In Wordle the object of the game is to guess a five letter word in six guesses or less. After each guess we are given three types of information:

• Correct characters in the correct position (green)
• Correct characters in the incorrect position (yellow)
• Incorrect characters (gray)

We can use this information to eliminate possible solutions and trim down our search space.

Zooming Out

Before we jump into our algorithm, let's look at the search space. We're going to grab two text files from github.

• Valid Wordle Guesses: 10,657 total words
• Valid Wordle Answers: 2,315 total words

These text files contain all valid wordle guesses and answers.

python
Copy Code
possible_guesses = set()

with open('wordle-allowed-guesses.txt', 'r') as words:
    for word in words.read().split():
        possible_guesses.add(word)

possible_answers = set()

with open('wordle-answers-alphabetical.txt', 'r') as words:
    for word in words.read().split():
        possible_answers.add(word)

wordle_words = possible_guesses | possible_answers

We now have a set of possible guesses and a set of possible answers. We can combine these to form a single set of valid Wordle words.

A Greedy Approach

I decided to take a greedy approach to solving Wordle. Greedy algorithms always choose the locally optimal solution at each step. While often effective, greedy algorithms are not guaranteed to always find the correct solution.

For Wordle, the locally optimal solution is the guess that eliminates the greatest number of words in the search space.

The general flow of the algorithm is:

• Determine the guess that eliminates the greatest number of words
• Make our guess
• Eliminate invalid words
• Repeat until solved

Now the question becomes, how do we determine the guess that eliminates the greatest number of words?

My solution was to create a metric that we can optimize as a proxy for the elimination of words. The metric that I came up with is the "character frequency score". This metric provides a relative ranking of all five letter words based on the frequency of each character. The words with the highest character frequency scores have the most common characters. Therefore if we optimize our guesses for the character frequency score, we should maximize the number of eliminations per guess.

Character Frequency Analysis

We'll start by computing the frequencies of each character in the alphabet for all five letter words in Wordle.

python
Copy Code
def compute_frequencies():
    frequencies = {} 
    percentages = {}
    alphabet = [chr(i) for i in range(97, 123)] # list with each character from a to z
    char_frequencies = {char: 0 for char in alphabet}
    char_percentages = {char: 0 for char in alphabet}
    total_chars = 0

    for word in wordle_words:
        for char in word:
            char_frequencies[char] += 1
            total_chars += 1
        for char in char_frequencies:
            if total_chars > 0:
                char_percentages[char] = char_frequencies[char] / total_chars
            else:
                char_percentages[char] = 0

    frequencies = char_frequencies
    percentages = char_percentages
    return frequencies, percentages

def plot_frequencies(frequencies):
    keys = list(frequencies.keys())
    values = list(frequencies.values())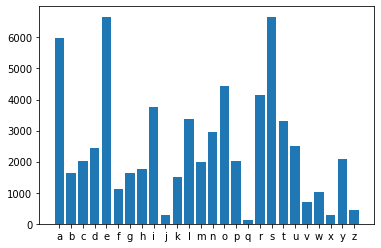
    x_pos = range(len(keys))
    plt.bar(x_pos, values)
    plt.xticks(x_pos, keys)
    plt.show()

frequencies, percentages = compute_frequencies()
plot_frequencies(frequencies)

This plot shows the distribution of characters for all five letter words in our dataset. We can see the most common characters include "a", "e", "s" and so on.

We can use this data to compute the character frequency score for each word. The character frequency score is the sum of the character frequency percentages for each unique character in a given word. This metric rewards words with unique characters by casting the word to a set and counting each character only once.

python
Copy Code
def get_frequency_score(word):
    return sum([percentages[char] for char in set(word)])
 
def sort_by_frequency_score(words):
    return sorted(words, key = lambda word: get_frequency_score(word))[::-1]

Here are the top five starting guesses in Wordle based on the character frequency score:

['arose', 'aeros', 'soare', 'reais', 'serai']

and the bottom five:

['immix', 'hyphy', 'gyppy', 'xylyl', 'fuffy']

Solving Wordle

We'll simulate a game of Wordle using the Game class below. The play method will execute the game loop, which will make a guess, update the eligible words, and repeat until the solution is found. I included a strategy field in the class and implemented a random guess strategy, which randomly selects from the remaining eligible words. The random guess strategy will provide a baseline of performance that we can compare against.

python
Copy Code
class Game:
    def __init__(self, strategy, word=''):
s       self.five_letter_words = wordle_words
        self.eligible_words = self.five_letter_words
        self.unique_char_map = {i: [] for i in range(1, 6)}
        self.yellow_positions = {i: set() for i in range(5)}
        if word == '':
            self.word = self.five_letter_words[np.random.randint(len(self.five_letter_words))]
        else:
            self.word = word
        self.strategy = strategy
        self.gray = set()
        self.yellow = ['_', '_', '_', '_', '_']
        self.green = ['_', '_', '_', '_', '_']
        self.guesses = []

    def summarize(self):
        print(self.green)
        print(self.yellow)
        print(self.gray)
        print(self.guesses)

    def guess(self, guess):
        self.guesses.append(guess)
        self.yellow = ['_', '_', '_', '_', '_']
        for i, char in enumerate(guess):
            if char not in self.word:
                self.gray.add(char)
            else:
                if char != self.word[i]:
                    self.yellow[i] = char
                    self.yellow_positions[i].add(char)
                else:
                    self.green[i] = char

    def optimize_frequency_score(self):
        return sort_by_frequency_score(self.eligible_words)[0]  

    def random_guess(self):
        return random.choice(list(self.eligible_words))

    def update_eligible_words(self):
        eligible = []
        for word in self.eligible_words:
            has_green_letters = True
            for i, char in enumerate(self.green):
                if char != '_' and word[i] != char:
                    has_green_letters = False
                    continue
            if not has_green_letters:
                continue
            has_yellow_letters = True
            for i, letters in self.yellow_positions.items():
                for char in letters:
                    if word[i] == char:
                        has_yellow_letters = False
                    if char not in word:
                        has_yellow_letters = False
            if not has_yellow_letters:
                continue
            does_not_have_gray_letters = True
            for char in self.gray:
                if char in word:
                    does_not_have_gray_letters = False
                    continue
            if does_not_have_gray_letters:
                eligible.append(word)
        self.eligible_words = eligible
        return self.eligible_words

    def play(self):
        solved = False
        while not solved:
            if self.strategy == 'random':
                guess = self.random_guess()
            elif self.strategy == 'optimize_frequency':
                guess = self.optimize_frequency_score()
            self.guess(guess)
            self.summarize()
            self.update_eligible_words()
            print(len(self.eligible_words))
            if '_' not in self.green:
                solved = True
        return len(self.guesses)

The last thing we need is some code to test our strategy on every possible Wordle answer and summarize the results.

python
Copy Code
def simulate(strategy):
    guesses = []

    for word in possible_answers:
        g = Game(strategy, word=word)
        guesses.append(g.play())

    average_guesses = sum(guesses) / len(guesses)
    six_or_fewer = 0
    for guess in guesses:
        if guess <= 6:
            six_or_fewer += 1

    six_or_fewer_percentage = six_or_fewer / len(guesses)
    data = Counter(sorted(guesses))
    print({i[0] : i[1] for i in sorted(data.items(), key=itemgetter(0))})
    keys = list(data.keys())
    values = list(data.values())
    x_pos = range(len(keys))
    plt.bar(x_pos, values)
    plt.xticks(x_pos, keys)
    plt.show()
    
    return average_guesses, six_or_fewer_percentage

Now for the moment of truth: let's see how our algorithm performs!

simulate('optimize_frequency')

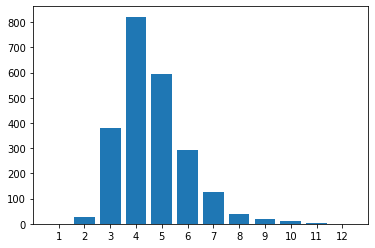
Average: 4.629

Six or Fewer Percentage: 91.5%

Our algorithm solves 91.5% of all Wordles, with an average of 4.6 guesses. Let's see how it compares to the random strategy.

simulate('random')

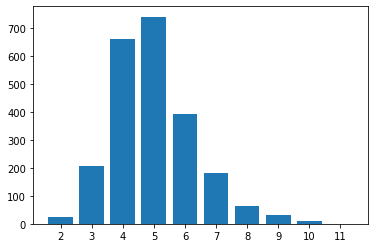
Average: 4.994

Six or Fewer Percentage: 87.6%

Our algorithm performed marginally better than the random strategy. This means that most of the performance comes from eliminating ineligible words after each guess. Optimizing the character frequency score resulted in a decrease of only 0.365 average guesses from the baseline.

Shortcomings

The main area where our algorithm fell short was handling words where there are many other eligible words that differ by only one or two characters.

For example, consider the word "roger". The list of guesses was:

['arose', 'oiler', 'noter', 'coder', 'moper', 'fouer', 'yoker', 'bower', 'hover', 'roger']

After two guesses we got to "_o_er" pattern with 39 eligible words remaining. From here, the algorithm continued to choose the word with the highest character frequency score. The problem is that there are too many words remaining, and we can only eliminate two characters at a time. All the cases on the right of the distribution have a similar pattern.

This is one of the shortcomings of a greedy algorithm. Sometimes the locally optimal choice does not lead to the globally optimal solution. In this case, the globally optimal choice would be a word that is not the right answer but that contains the most unused characters.

Improvements

The character frequency score is just one metric of countless that we can optimize, and optimization of a single metric is only one strategy of many. I expect a dynamic guessing strategy that optimizes different metrics depending on the number of remaining guesses would probably be most effective.

For now we can continue to enjoy the uncertainty of that remaining 8.5% that makes Wordle fun.